Assessment of unsteady flow predictions using hybrid deep learning based reduced-order models

Abstract

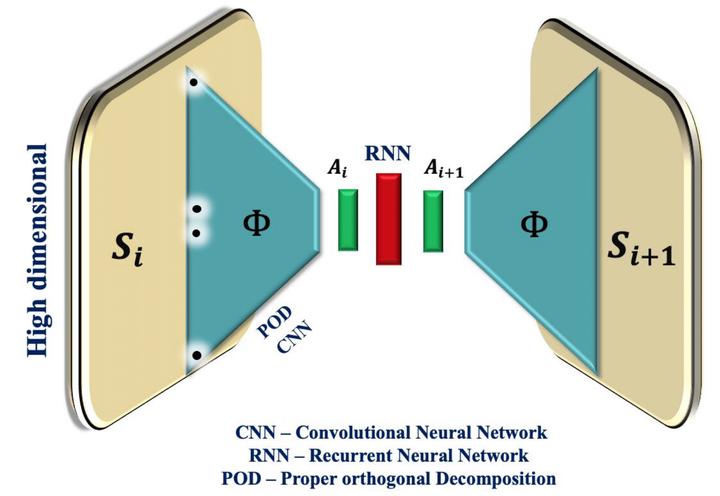
In this paper, we present two deep learning-based hybrid data-driven reduced-order models for prediction of unsteady fluid flows. These hybrid models rely on recurrent neural networks (RNNs) to evolve low-dimensional states of unsteady fluid flow. The first model projects the high-fidelity time series data from a finite element Navier–Stokes solver to a low-dimensional subspace via proper orthogonal decomposition (POD). The time-dependent coefficients in the POD subspace are propagated by the recurrent net (closed-loop encoder–decoder updates) and mapped to a high-dimensional state via the mean flow field and the POD basis vectors. This model is referred to as POD-RNN. The second model, referred to as the convolution recurrent autoencoder network (CRAN), employs convolutional neural networks (instead of POD) as layers of linear kernels with nonlinear activations, to extract low-dimensional features from flow field snapshots. The flattened features are advanced using a recurrent (closed-loop manner) net and up-sampled (transpose convoluted) gradually to high-dimensional snapshots. Two benchmark problems of the flow past a cylinder and the flow past side-by-side cylinders are selected as the unsteady flow problems to assess the efficacy of these models. For the problem of the flow past a single cylinder, the performance of both the models is satisfactory and the CRAN model is found to be overkill. However, the CRAN model completely outperforms the POD-RNN model for a more complicated problem of the flow past side-by-side cylinders involving the complex effects of vortex-to-vortex and gap flow interactions. Owing to the scalability of the CRAN model, we introduce an observer-corrector method for calculation of integrated pressure force coefficients on the fluid–solid boundary on a reference grid. This reference grid, typically a structured and uniform grid, is used to interpolate scattered high-dimensional field data as snapshot images. These input images are convenient in training the CRAN model, which motivates us to further explore the application of the CRAN-based models for prediction of fluid flows.

Sandeep Reddy B

Research Scientist

My research interests include data-driven computing, model order reduction, physics informed A.I and nonlinear systems.